Model Explainability with SHapley Additive exPlanations (SHAP)

Source

One of the big criticisms of modern machine learning is that it's essentially a blackbox -- data in, prediction out, that's it. And in some sense, how could it be any other way? When you have a highly non-linear model with high degrees of interactions, how can you possibly hope to have a simple understanding of what the model is doing? Well, turns out there is an interesting (and practical) line of research along these lines.

This post will dive into the ideas of a popular technique published in the last few years call SHapely Additive exPlanations (or SHAP). It builds upon previous work in this area by providing a unified framework to think about explanation models as well as a new technique with this framework that uses Shapely values. I'll go over the math, the intuition, and how it works. No need for an implementation because there is already a nice little Python package! Confused yet? Keep reading and I'll explain.


Shapely Values and Cooperative Games

Cooperative Games

Imagine you're on a reality TV show where you're stuck on a desert island with two other people. The longer all of you stay on the island, the more money you will all make. You need to work together in order to maximize your return. Your payoff will change significantly depending on whom you're with. In this scenario, of course, you want to pick the two best people to bring with you, but how to choose? For example, you probably want to pick someone who has extensive survivability experience, they would obviously contribute a lot to a better outcome. On the other hand, you probably don't want to pick someone like me who spends the majority of their free time indoors in front a computer, I might just be dead weight. In essence, we want to answer two questions:

  1. How important is each person to the overall goal of surviving longer (i.e. what's their fair share of the winnings)?

  2. What outcome can we reasonably expect?

This is essentially the problem of a cooperative game from game theory (this is in contrast to the traditional non-cooperative games from game theory that most people are familiar with). Formally:

A coalitional game is a where there is a set \(N\) players and a value function \(v\) that maps each subset of players to a payoff. Formally, \(v: 2^N \rightarrow \mathbb{R}\) with \(v(\emptyset)=0\) (empty set is zero).

The value function \(v(S)\) describes the total expected payoff for a subset of players \(S\). For example, including a survivalist in your desert island coalition will likely result in better outcome (payoff) than including me. This function answers the second question: what outcome can we reasonably expect (given a subset of players)?

So far we've just setup the problem though. Now we want to answer the question: what should be everyone's "fair" distribution of the total payoff? In other words, the first question: how much does each person contribute to the overall goal. Clearly, the survivalist should get more more of the payout than me, but how much more? Is there only one "unique" solution? The answer lies in Shapely values.

Shapely Values 1

Shapely values (named in honour of Lloyd Shapely), denoted by \(\varphi_i(v)\), are a solution to the above coalition game. For player \(i\) and value function \(v\), the Shapely value is defined as:

\begin{align*} \varphi_i(v) &= \frac{1}{N} \sum_{S \subseteq N \setminus \{i\}} {N-1 \choose |S|}^{-1} (v(S\cup \{i\}) - v(S)) \tag{1} \\ &= \frac{1}{\text{number of players}} \sum_{\text{coalitions excluding }i} \frac{\text{marginal contribution of i to coalition}}{\text{number of coalitions excluding i of this size}} \\ &= \sum_{S \subseteq N \setminus \{i\}} \frac{|S|!(N-|S|-1)!}{N!} (v(S\cup \{i\}) - v(S)) \tag{2} \end{align*}

This definition is quite intuitive: average over your marginal contribution in every possible situation. Equation 1 shows this intuition the best where you take the incremental benefit of including player \(i\) and average over every possible subset that could include player \(i\). Equation 2 is a simplification that you might see more often, which is just expanding the combination and simplifying.

Shapely values are also a very nice because they are the only solution with these desirable properties:

  1. Efficiency: The sum of Shapely values of all agents is equal to the total for the grand coalition:

    \begin{equation*} \sum_{i\in N} \varphi_i(v) = v(N) \end{equation*}

  2. Symmetry: If \(i\) and \(j\) are two players who are equivalent in the sense that

    \begin{equation*} v(S \cup \{i\}) = v(S \cup \{j\}) \end{equation*}

    for every subset \(S\) of \(N\) which contain neither \(i\) nor \(j\), then \(\varphi_i(v) = \varphi_j(v)\).

  3. Linearity: Combining two coalition games \(v\) and \(w\) is linear for every \(i\) in \(N\):

    \begin{align*} \varphi_i(v+w) = \varphi_i(v) + \varphi_i(w) \\ \varphi_i(av) = a\varphi_i(v) \end{align*}

  4. Null Player: For a null player, defined as \(v(S\cup \{i\})=v(S)\) for all coalitions \(S\) not containing \(i\), then \(\varphi_i(v) = 0\).

All of these properties seem like pretty obvious things you would want to have:

  • Efficiency: Of course, you want your distribution across players to actually sum up to the total reward.

  • Symmetry: If two people contribute the same to the game, you want them to have the same payoff.

  • Linearity: If a game is composed of two independent sub-games, you want the total game to be the sum of the two games.

  • Null Player: If a player contributes nothing, then their share should be nothing.

Let's take a look at a couple examples to get a feel for it.

Example 1: Glove Game

Imagine we have a game where players have left or right handed gloves. The goal is to form pairs. Imagine a three player game: \(N=\{1,2,3\}\) where Players 1 and 2 have left handed gloves and Player 3 has a right handed glove. The value function is scoring for every subset that has a L/R pair, and zero otherwise:

\begin{equation*} v(S) = \begin{cases} 1 & \text{if } S \in \{\{1,3\}, \{2,3\}, \{1,2,3\}\} \\ 0 & \text{otherwise} \end{cases} \end{equation*}

Using Equation 1, we need to find the marginal contribution of players. For Player 1, we have:

\begin{align*} v(\{1\}) - v(\emptyset) &= 0 - 0 &= 0 \\ v(\{1,2\}) - v(\{2\}) &= 0 - 0 &= 0 \\ v(\{1,3\}) - v(\{3\}) &= 1 - 0 &= 1 \\ v(\{1,2,3\}) - v(\{2, 3\}) &= 1 - 1 &= 0 \end{align*}

From Equation 1:

\begin{align*} \varphi_1(v) &= \frac{1}{N} \sum_{S \subseteq N \setminus \{i\}} {N-1 \choose |S|}^{-1} (v(S\cup \{i\}) - v(S)) \\ &= \frac{1}{3} \big[{2 \choose 0}^{-1} (v(\{1\}) - v(\emptyset)) + {2 \choose 1}^{-1} (v(\{1,2\}) - v(\{2\})) + \\ &\hspace{2.3em} {2 \choose 1}^{-1} (v(\{1,3\}) - v(\{3\})) + {2 \choose 2}^{-1} (v(\{1,2,3\}) - v(\{,,3\})) \big] \\ &= \frac{1}{3}[1(0) + \frac{1}{2}(0) + \frac{1}{2}(1) + (1)(0)] \\ &= \frac{1}{6} \\ \tag{3} \end{align*}

Based on symmetry (Property 2), we can conclude Player 1 and 2 are equivalent, so:

\begin{align*} \varphi_2(v) = \varphi_1(v) = \frac{1}{6} \\ \tag{4} \end{align*}

Further, due efficiency (Property 1), we can find the remaining Shapely value for Player 3:

\begin{align*} \varphi_3(v) = v(N) - \varphi_1(v) - \varphi_3(v) = 1 - \frac{1}{6} - \frac{1}{6} = \frac{2}{3} \\ \tag{5} \end{align*}

As expected, since Player 3 has the only right handed glove, so their split of the profits should be 4 times bigger than the other players.

Example 2: Business

Consider an owner of a business, denoted by \(o\), who provides the initial investment in the business. If there is no initial investment, then there is no business (zero return). The business also has \(k\) workers \(w_1, \ldots, w_k\), each of whom contribute \(p\) to the overall profit. Our set of players is:

\begin{equation*} N = \{o, w_1, \ldots, w_k\} \tag{6} \end{equation*}

The value function for this game is:

\begin{align*} v(S) = \begin{cases} mp & \text{if } o \in S \\ 0 & \text{otherwise } \end{cases} \\ \tag{7} \end{align*}

where \(m\) is the number of players in \(S \setminus o\).

We can setup Equation 1 but breaking down the sum into symmetrical parts based on the size of \(S\):

\begin{align*} \varphi_{o}(v) &= \frac{1}{N} \sum_{S \subseteq N \setminus \{o\}} {N-1 \choose |S|}^{-1} (v(S\cup \{o\}) - v(S)) \\ &= \frac{1}{N} \big[ \sum_{m=1}^k \sum_{S \subseteq N \setminus \{o\}, |S|=m} {N-1 \choose |S|}^{-1} (v(S\cup \{o\}) - v(S)) \big] \\ &= \frac{1}{N} \big[ \sum_{m=1}^k {N-1 \choose |S|}^{-1} {N-1 \choose |S|} mp \big] && \text{each of the inner summations is symmetric}\\ & && \text{and } v(S)=0 \text{ since there is no owner}\\ &= \frac{1}{N} \sum_{m=1}^k mp \\ &= \frac{1}{k+1} \frac{k(k+1)p}{2} && \text{N=k+1}\\ &= \frac{kp}{2} \\ \tag{8} \end{align*}

By efficiency and symmetry, the rest of the k workers get the rest of the \(\frac{kp}{2}\) profits (total profits is \(kp\)), and thus each worker should get \(\frac{p}{2}\) of the profits. In other words, each worker is "contributing" half of their share of the profits they make to the business owner.

Is it fair though? Shapely values seems to say so. Whether this has any implications for our capitalistic society where investors/business owners get much more than half of the profits is left as an exercise for the reader :p


Feature Explainability as Shapely Values

Additive Feature Attribution Models

The first thing we need to cover is what does it mean for a model to be explainable? Take a simple linear regression for example:

\begin{equation*} y = \beta_0 + \beta_1 x_1 + \ldots + \beta_n x_n \tag{9} \end{equation*}

This model probably follows our intuition of an explainable model: each of the \(x_i\) variables are independent, additive, and we can clearly point to a coefficient (\(\beta_i\)) saying how it contributed to the overall result (\(y\)). But what about more complex models? Even if we stick with linear models, as soon as we introduce any interactions, it gets messy:

\begin{equation*} y = \beta_0 + \sum_{i=1}^n \beta_i x_i + \sum_{i=1}^{n-1} \sum_{j>i}^{n} \beta_{i,j}x_i x_j \tag{10} \end{equation*}

In this case, how much has \(x_i\) contributed to the overall prediction? I have no idea and the reason is that my intuition expects the variables to be independent and additive, and if they're not, I'm not really sure how to "explain" the model.

So far we've been trying to explain the model as a whole. What if we did something simpler? What if instead of trying to explain the entire model, we took on a simpler problem: explain a single data point. Of course, we would want some additional properties, namely, that we can interpret it like the simple linear regression in Equation 9, that there is some guarantee of local accuracy, and probably some guarantee that similar models would produce similar explanations. We'll get to all of that but first let's setup the problem and go through some definitions.

What we are describing here are called local methods designed to explain a single input \(\bf x\) on a prediction model \(f({\bf x})\). When looking to explain a single data point, we don't really care about the level (i.e. value) of a feature, just how much its presence contributes to the overall prediction. To that end, let's define a binary vector of simplified inputs \(\bf x'\) (denoted by \('\)) that represents whether or not we want to include that feature's contribution to the overall prediction (analogous to our cooperative game above). We also have a mapping function \(h_x({\bf x'}) = {\bf x}\) that translates this binary vector to the equivalent values for the data point \(\bf x\). Notice that this mapping function \(h_x(\cdot)\) is specific to data point \(x\) -- you'll have one of these functions for every data point. It's a bit confusing to write out in words so let's take a look at an example which should clarify the idea.

Example 3: Simplified Inputs

Consider a simple linear interaction model with two real inputs \(x_1, x_2\):

\begin{equation*} y = 1 + 2 x_1 + 3 x_2 + 4 x_1 x_2 \tag{11} \end{equation*}

Let's look at two data points:

\begin{align*} {\bf u} &= (x_1, x_2) = (-1, -0.5), &&y = -0.5 \\ {\bf v} &= (x_1, x_2) = (0.5, 1), &&y = 7 \\ \tag{12} \end{align*}

Let's suppose we wanted to look at the effect of \(x_1\) for these two data points. We would look at the vector \({\bf z'} = [1, 0]\) (where \(z \in \{u, v\}\)) and use their \(h\) mapping to find the original values:

\begin{align*} h_{\bf u}({\bf z'}) = h_{\bf u}([1, 0]) = [-1, n/a] \\ h_{\bf v}({\bf z'}) = h_{\bf v}([1, 0]) = [0.5, n/a] \\ \tag{13} \end{align*}

where we represent missing values with "n/a" (we'll get to this later). As you can see, this formalism allows us to speak about whether we should include a feature or not and their equivalent values.

Now that we have these definitions, our end goal is to essentially build a new explanation model, \(g({\bf z'})\) that ensures that \(g({\bf z'}) \approx f(h_{\bf x}({\bf z'}))\) whenever \({\bf z'} \approx {\bf x'}\). In particular, we want this explanation model to be simple like our linear regression in Equation 9. Thus, let's define this type of model:

Additive Feature Attribution Methods have an explanation model that is a linear function of binary variables:

\begin{equation*} g({\bf z'}) = \phi_0 + \sum_{i=1}^M \phi_i z_i' \tag{14} \end{equation*}

where \(z' \in \{0,1\}^M\), \(M\) is the number of simplified input features and \(\phi_i \in \mathbb{R}\).

This essentially captures our intuition on how to explain (in this case) a single data point: additive and independent. Next, we'll look at some desirable properties that we want to maintain in this mapping.

Desirable Properties and Shapely Values

The first property we would want from our point-wise explanation model \(g(\cdot)\) is some guarantee of local accuracy:

Property 1 (Local Accuracy)

\begin{equation*} f(x) = g({\bf x'}) = \phi_0 + \sum_{i=1}^M \phi_i x_i' \tag{15} \end{equation*}

The explanation model \(g\) matches the original model when \(x = h_x(x')\), where \(\phi_0 = h_x({\bf 0})\) represents the model output with all simplified inputs toggled off.

All this property is saying is that if you pass in the original data point with all features included (\(x\)), your explanation model (\(g\)) should return the original value of your model (\(f\)), seems reasonable.

Property 2 (Missingness)

\begin{equation*} x_i' = 0 \implies \phi_i = 0 \tag{16} \end{equation*}

Missing input features in the original data point (\(x_i\)) have no attributed impact.

This property almost seems unnecessary because all it is saying is that if your original data point doesn't include the variable ("missing") then it shouldn't show any attributed impact in your explanation model. The idea of a "missing" input is still something we have to deal with because most models don't really support missing feature columns. We'll get to it in the next section.

Property 3 (Consistency): Let \(f_x(z') = f(h_x(z'))\) and \(z' \backslash i\) denote setting \(z_i'=0\). For any two models \(f\) and \(f'\), if

\begin{equation*} f_x'(z')-f_x'(z' \backslash i) \geq f_x(z')-f_x(z' \backslash i) \tag{17} \end{equation*}

for all inputs \(z'\in {0,1}^M\) then \(\phi_i(f', x) \geq \phi_i(f,x)\).

This is a more important property that essentially says: if we have two (point-wise) models (\(f, f'\)) and feature \(i\) consistently contributes more to the output in \(f'\) compared to \(f\), we would want the coefficient of our explanation model for \(f'\) to be bigger than \(f\) (i.e. \(\phi_i(f', x) \geq \phi_i(f,x)\)). It's a sensible requirement that allows us to fairly compare different models using the same explainability techniques.

These three properties lead us to this theorem:

Theorem 1 The only possible explanation model \(g\) following an additive feature attribution method and satisfying Properties 1, 2, and 3 are the Shapely values from Equation 2:

\begin{equation*} \phi_i(f,x) = \sum_{z'\subseteq x'} \frac{|z'|!(M-|z'|-1)!}{M!}[f_x(z')-f_x(z' \backslash i)] \tag{18} \end{equation*}

This is a bit of a surprising result since it's unique. Interestingly, some previous methods (e.g. Lime) don't actually satisfy all of these conditions such as local accuracy and/or consistency. That's why (at least theoretically) Shapely values are such a nice solution to this feature attribution problem.

SHapely Additive exPlanations (SHAP)

If it wasn't clear already, we're going to use Shapely values as our feature attribution method, which is known as SHapely Additive exPlanations (SHAP). From Theorem 1, we know that Shapely values provide the only unique solution to Properties 1-3 for an additive feature attribution model. The big question is how do we calculate the Shapely values (and what do they intuitively mean)?

Recall that Shapely values rely on the value function, \(v(S)\), which determine a mapping from a subset of features to an expected "payoff". In the case of Equation 18, our "payoff" is the model prediction \(f_x(z')\) i.e. the prediction of our model at point \(x\) with subset of features \(z'\). Implicit in this definition is that we can evaluate our model with just a subset of features (i.e. the value function), which most models do not support. So how does SHAP deal with it? Expectations!

To evaluate a model at point \(x\) with a subset of features \(S\), it starts out with the expectation of the function (recall, \(z'\) is our binary vector representing \(S\) and \(h_x(\cdot)\) is the mapping from the binary vector to the actual features in data point \(x\)):

\begin{align*} f(h_x(z')) &= E[f(z)|z_S] \\ &= E_{z_{\bar{S}}|z_S}[f(z)] \\ \tag{19} \end{align*}

There are two main issues with this. First, most models don't have an explicit probability density, nor do they know how to deal with missing values, so we have to approximate it using our dataset. Depending on the model, this may be easy or hard to compute. For example, if our data point is describing a customer and we had one missing dimension, it might look like this:

\begin{align*} {\bf x}&=\{x_{sex}=M, x_{age=18}, x_{spending}=100, x_{recency}=2, x_{location}=City, \ldots\} \\ {\bf x_{\overline{sex}}}&=\{x_{sex}=N/A, x_{age=18}, x_{spending}=100, x_{recency}=2, x_{location}=City, \ldots\} \\ \tag{20} \end{align*}

To compute the value of the function missing the feature \(x_{sex}\), we could simply just average over all the data points that included it, holding all the other variables constant. This would approximate the expectation \(E[f(z)|z_S]\). Of course, our estimate of this value could be wildly off if you don't have enough data so we won't always do this explicitly.

The second issue is that if you look back at Equation 18 you realize that we would have to compute this expectation for every subset of features, which is exponential in the number of features! This is definitely a big barrier to any practical application of this technique. Often times we will just sample from the power set of features to approximate it (see Kernel SHAP), in other cases we can calculate it precisely because of the type of model. More on this later.

We can also make two simplifications to deal with the missingness issue: independence and linearity.

\begin{align*} f(h_x(z')) &= E[f(z)|z_S] \\ &= E_{z_{\bar{S}}|z_S}[f(z)] \tag{21} \\ &\approx E_{z_{\bar{S}}}[f(z)] && \text{independence} \tag{22} \\ &\approx f(z_S, E[z_{\bar{S}}]) && \text{linear} \tag{23} \end{align*}

Independence allows us to treat each dimension separately and not care about the conditional aspect of trying to find a data point that "matches" \(x\) (such as in Equation 20). We can simply sample values from the missing dimension(s) independently to fill the "N/A"s and average over them to estimate the expectation. Of course, this will only really work out if we actually have feature independence, otherwise we're likely to sample values from the missing dimensions that create unlikely data points that don't really represent the underlying distribution.

Linearity additionally allows us to simply compute the expectation (\(E[z_{\bar{S}}]\)) over each dimension of \(x\) separately and plug it into the model, removing the need to do sampling to estimate the expectation.

To summarize, we can calculate feature importance by:

  1. Computing Shapely values as in Equation 18:

    \begin{equation*} \phi_i(f,x) = \sum_{z'\subseteq x'} \frac{|z'|!(M-|z'|-1)!}{M!}[f_x(z')-f_x(z' \backslash i)] \end{equation*}

    which is often estimated by sample subsets from the power set of features (Kernel SHAP).

  2. To evaluate the model with "missing" values (\(f_x(z')\)), we will use our dataset to approximate the expectation \(f_x(z') = E[f(z)|z_S]\). We will often assume independence and linearity, which allows us to greatly simplify the computation needed.

Now this leaves us with two additional questions: how do we interpret these feature importances? And how can we compute these values efficiently for different types of models. We'll get to the first question in the next subsection and the latter in the next section.

Interpreting SHAP Feature Importances

SHAP features get us close but not quite the simplicity of a linear model in Equation 9. The big difference is that we are analyzing things on a per data point basis as opposed to Equation 9 where we are doing it globally over the entire dataset. Also recall that SHAP is based on Shapely values, which are averages over situations with and without the variable, leading us to contrastive comparisons with the base case (no features/players). Figure 1 from the SHAP paper shows a visualization of this concept.

SHAP Values

Figure 1: SHAP Values [1]

Here are some notes on interpreting this diagram:

  • Notice that \(\phi_0\) is simply the expected value of the overall function. This is complete "missing"-ness. If you are missing all features, then the value you should use as a "starting point" or base case is just the mean of the prediction over the entire dataset. Isn't this more logical (with respect to the dataset) than starting at 0? This is sort of analgous to the linear regression case except the intercept in linear regression is the mean when all inputs are zero. We have to have a different definition here because missing a features is not the same thing as zeroing it out.

  • Looking at the calculated line segments in the diagram, you can see that each value is calculated as the difference between an expectation relative to some conditional value and the same expectation less one variable. This is a realization of Equation 18 where \(f_x(z)-f_x(z \backslash i) = E[f(z) | z] - E[f(z) | z \backslash i]\).

  • The figure assumes independence and linearity because it associates \(\phi_i\) with one particular ordering of variables (e.g. \(\phi_2 = E[f(z)|z_{1,2}]=x_{1,2} - E[F(z)|z_1=x_1]\)). If we didn't have these assumptions, we would have to calculate \(\phi_i\) as in Equation 18 where \(\phi_i\) would be averaged over all possible subsets that include/exclude that variable.

  • The arrows corresponding to \(\phi_i\) are sequenced additively to sum up to the final prediction. That is, SHAP generates an additive model where each feature importance can be additively summed to generate the final prediction (Property 1). This is true regardless of whether you have linearity and independence as shown in the diagram, or you have to sum over all possible subsets as in Equation 18 (in the latter case the diagram would look different).

The SHAP values can be confusing because if you don't have the independence and linearity assumptions, it's not very intuitive the calculate (it's not easy visualizing averages over all possible subsets). The important point here is that they are contrastive, which means we can compare their relative value to each other fairly but they don't have the same absolute interpretations as linear regression. This is most clearly seen by the fact that every \(\phi_{i\neq0}\) is relative to \(\phi_0\), the mean prediction of your dataset. Having a feature importance of \(\phi_i=10\) does not mean including the feature contributes \(10\) to your prediction, it means relative to the average prediction, it adds \(10\). I suspect that there is some manipulation you can do to approximately get that "absolute" type of feature importance that we see in linear regression but I haven't fully figured it out yet.

Let's take a look at the same visualization as above but from the visualization that the SHAP Python package [3] provides (Figure 2):

SHAP Values

Figure 2: SHAP Values from the SHAP Python package [3]

We can see the same idea as Figure 1, however we don't assume any particular ordering, instead we just stack all the positive feature importances to the left, and all negative to the right to arrive at our final model prediction of \(24.41\). Rotating Figure 2 by 90 degrees and stacking all possible values side-by-side, we get Figure 3.

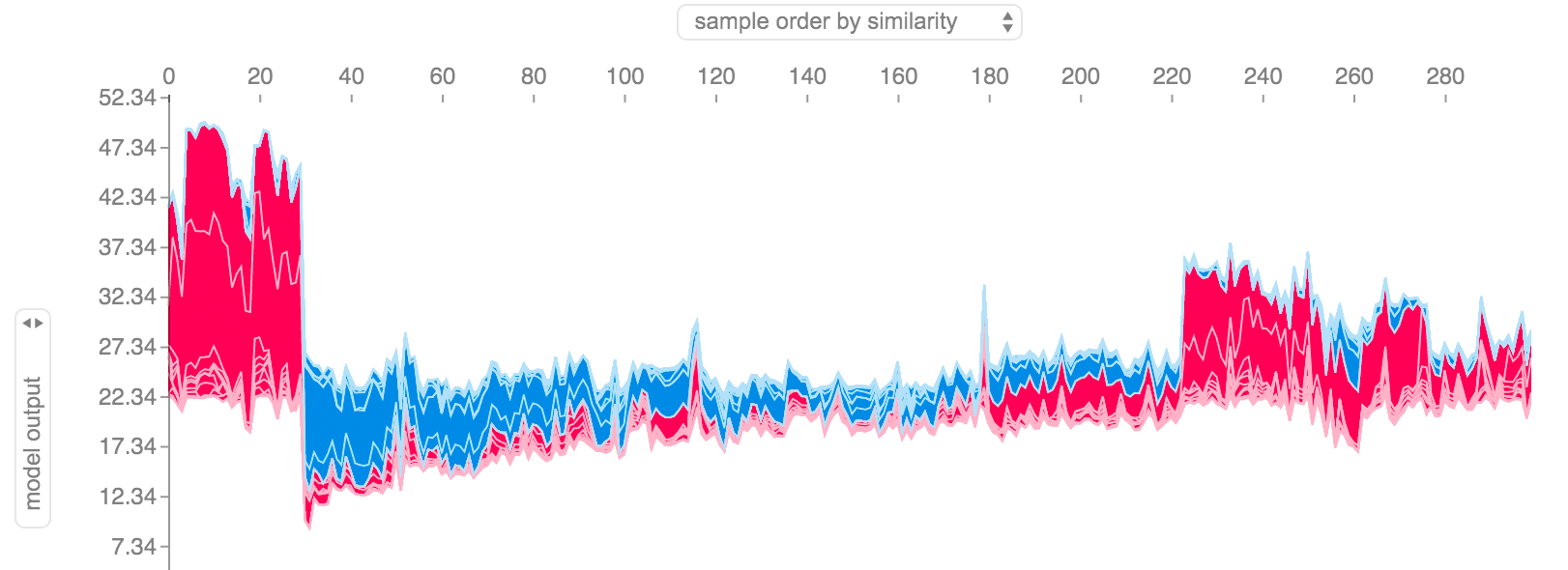
SHAP Values

Figure 3: SHAP Values from the SHAP Python package for entire dataset [3]

Figure 3 shows a global view of all possible data points and their SHAP contributions relative to the overall mean (\(22.34\)). The plot is actually interactive (when created in a notebook) so you can scroll over each data point and inspect the SHAP values.

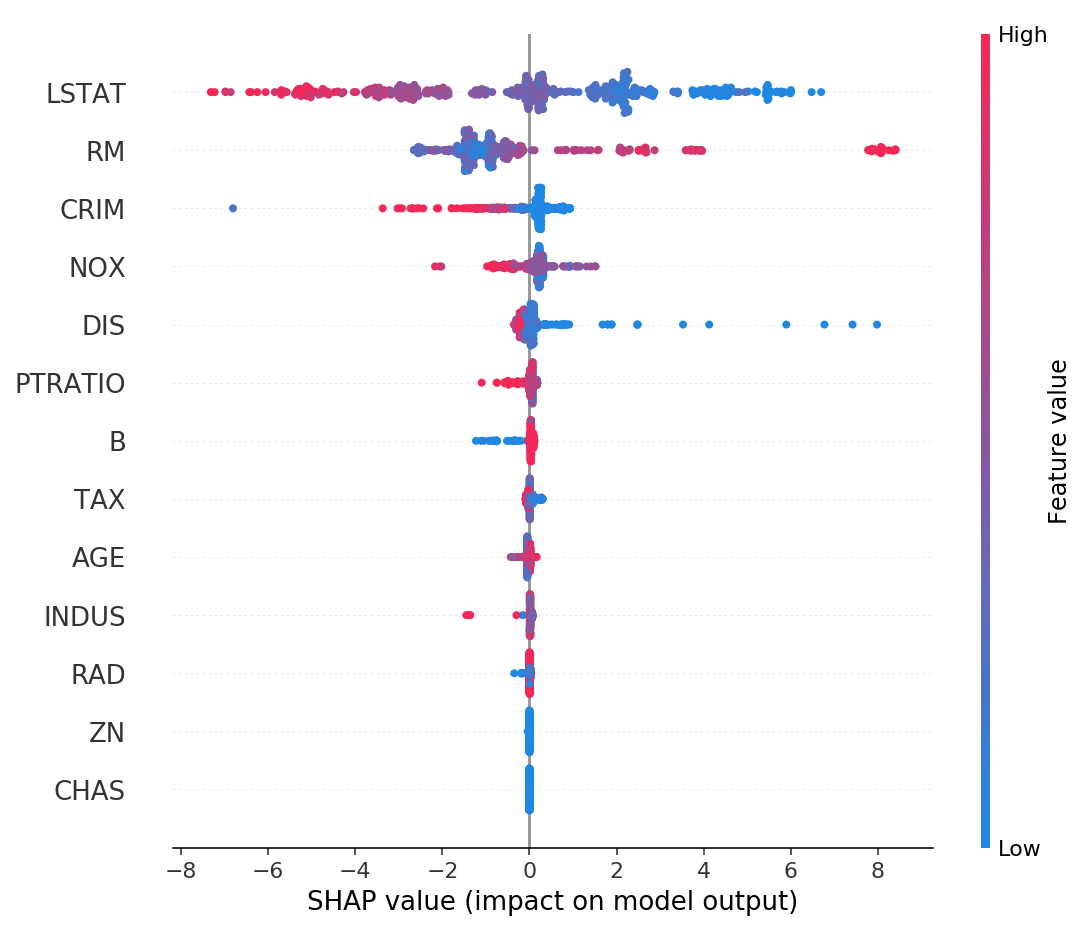
SHAP Values

Figure 4: Summary of SHAP values over all features [3]

Figure 4 shows another global summary of the distribution of SHAP values over all features. For each feature (horizontal rows), you can see the distribution of feature importances. From the diagram we can see that LSTAT and RM have large effects on the prediction over the entire dataset (high SHAP value shown on bottom axis). High LSTAT values affect the prediction negatively (red values on the left hand side), while high RM values affect the prediction positively (red values on the right hand side), similarly in the opposite direction for both variables.

SHAP Summary

As we can see the SHAP values are very useful and have some clear advantages but also some limitations:

  • Fairly distributed, Contrastive Explanations: Each feature is treated the same without any need for heuristics or special insight by the user. However, as mentioned above the explanations are contrastive (relative to the mean), so not exactly the same as our simple linear regression model.

  • Solid Theoretical Foundation: As we can see from above, almost all of the preamble was defining the theoretical foundation, culminating in Theorem 1. This is nice since it also frames certain other techniques (e.g. LIME) in a new light.

  • Global model interpretations: Unlike other methods (e.g. LIME), SHAP can provide you with global interpretations (as seen in the plots above) from the individual Shapely values for each data point. Moreover, due to the theoretical foundations and the fact that Shapely values are fairly distributed, we know that the global interpretation is consistent.

  • Fast Implementations: Practically, SHAP would only be useful if it were fast enough to use. Thankfully, there is a fast implementations if you are using a tree-based model, which we'll discuss in the next section. However, the model agnostic versions utilize the independence assumption and can be slow if you want to use it globally on the entire dataset (but work well enough on a single data point).

If you want a more in-depth treatment, [4] is an amazing reference summarizing SHAP and many other techniques.


Computing SHAP

Now that we've covered all the theoretical aspects, let's talk about how it works practically. Practically, you don't need to do much: there is a great Python package ([3]) by the authors of the SHAP paper that takes care of everything. But there are definitely nuances that you should probably know when using the different APIs. Let's take a look at the common methods and see how they differ.

Linear Models

For linear models, we can directly compute the SHAP values which are related to the model coefficients.

Corollary 1 (Linear SHAP): Given a model \(f(x) = \sum_{j=1}^M w_jx_j + b\) then \(\phi_0(f,x)=b\) and \(\phi_i(f,x) = w_j(x_j-E[x_j])\).

As you can see there is a simple mapping from linear coefficients to SHAP values. The reason why they are not equal is that SHAP is contrastive, that is its feature importance is compared to the mean. That's why we have that extra term in the SHAP value \(\phi_i\).

Kernel SHAP (Model Agnostic)

Many times we don't have the luxury of just using a linear model and have to use something more complex. In this case, we can compute things using a model agnostic technique called Kernel SHAP, which is a combination of LIME ([5]) and Shapely values.

The basic idea here is that for each data point under analysis, we will:

  1. Sample different coalitions of including the feature/not including the feature i.e. \(z_k' \in \{0,1\}^M\), where \(M\) is the number of features.

  2. For each sample, get the prediction of \(z_k'\) by applying our mapping function on our model (i.e. \(f(h_x(z_k'))\)), using the assumption that the missing values are replaced with randomly sampled values for that dimension (the independence assumption). It's possible to additionally assume linearity too, where we would replace the value with the mean of that dimension or equivalent. For example, in an image you might replace a pixel with the mean of the surrounding pixels (see [4] for more details).

  3. Compute a weight for each data point \(z_k'\) using the SHAP kernel: \(\pi_{x'}(z')=\frac{(M-1)}{{M \choose |z'|}|z'|(M-|z'|)}\).

  4. Fit a weighted linear model (see [1] for details)

  5. Return the coefficients of the linear model as the Shapely values (\(\phi_k\)).

The intuition here is that we can learn more about a feature if we study it in isolation. That's why the SHAP kernel will weight having a single feature, or correspondingly M-1 features, more heavily (the denominator is largest when \(M \choose |z'|\) is small). When \(|z'|=0\) or \(|z'|=M\) the expression has a divide by zero, but you can just drop these terms in general (that's how I interpret what the paper says anyways).

The good part is that this technique works with any model. However, it's relatively slow since we have to sample a bunch of values for each data point in our training set and fit a linear regression. We also have to use the independence assumption, which can be violated when our actual model does not have feature independence. This might lead to violations in the local accuracy or consistency guarantees.

TreeSHAP

TreeSHAP [2] is a decision tree-specific algorithm to compute SHAP. Due to the nature of decision trees, it doesn't need to use the independence (or linear) assumptions. Furthermore, due to some clever optimization, it can actually be computed in \(O(TLD^2)\) time where \(T\) is the number of trees, \(L\) is the number of leaves and \(D\) is the depth. So as long as you don't have gigantic trees, it scales very well.

The crux of the algorithm is computing precisely \(E[f(x)|x_s]\) (Equation 21), which can be done recursively and shown below in Figure 5. Vectors \(a\) and \(b\) represent the left and right node indexes for each internal node, \(t\) the thresholds for each node, and \(d\) is the vector of features used for splitting. \(r\) represents the cover for each vector i.e. how many data samples are in that sub-tree.

Naive TreeSHAP Algorithm

Figure 5: Naive TreeSHAP Algorithm [2]

This naive algorithm is pretty straight-forward to understand. It recursively traverses the tree and either follows a branch if you are conditioning on a variable (\(x_s\)), otherwise computes a weighted average of the two branches based on the number of data samples (the expectation). It works because decision trees are explicitly sequential in how they compute their values, so "skipping" over a missing variable is easy: just jump over that level of the tree by doing a weighted average over it.

One thing you'll notice is that computing SHAP values using Figure 5's algorithm is very expensive, on the order of \(O(TLM2^M)\). Exponential in the number of features! The exponential part comes from the fact that we still need to compute all subsets of \(M\) features, which means running the algorithm \(2^M\) times. It turns out we can do better.

A more complex algorithm which is shown in [2] tries to keep track of all possible subsets as it traverses down the tree. The algorithm is quite complex and, honestly, I don't quite understand (or care to understand) all the details at this point so I'll leave it as an exercise to the reader. The more interesting thing about this algorithm is that it runs in \(O(TLD^2)\) time and \(O(D^2+M)\) memory. Since we're only doing one traversal of the tree, we get rid of the exponential number of calls but require more computation to account for all the different subsets. The extension to simple ensembles of trees is pretty straight forward. Since common algorithms like random forests or gradient boosted trees are additive, we can simply compute the SHAP value for each tree independently and add them up.

Other SHAP Methods

The papers by the original authors in [1, 2] show a few other variations to deal with other model like neural networks (Deep SHAP), SHAP over the max function, and quantifying local interaction effects. Definitely worth a look if you have some of those specific cases.


Conclusion

With all the focus on deep learning in the recent years, it's refreshing to see really impactful research in other fields, especially the burgeoning field of explainable models. It's especially important in this day and age of blackbox models. I also like the fact that there was some proper algorithmic work with the TreeSHAP paper. The work of speeding up a naive algorithm from exponential to low-order polynomial reminds me of my grad school days (not that I ever had a result like that, just the focus on algorithmic work). Machine learning is definitely a very wide field and the reason why it's so interesting is that you have to constantly pull from so many different disciplines to understand it (to a satisfactory degree). See you next time!


References

1

This treatment of Shapely values is primarily a re-hash of the corresponding Wikipedia article. It's actually written quite well, so you should go check it out!

Hi, I'm Brian Keng. This is the place where I write about all things technical.

Twitter: @bjlkeng


Signup for Email Blog Posts